W poprzednim odcinku liznęliśmy trochę mechaniki klasycznej i kwantowej, dziś zajmiemy się chaosem i motylkami.
Wiemy już, że wszechświat fizyczny według Newtona działa według zbioru trzech stałych praw, a każde działanie jest zdeterminowane i można je przewidzieć zarówno wstecz, jak i w przód w czasie.
W XIX wieku Henri Poincare badał zachowywanie się obiektów astronomicznych. Początkowa niepewność pomiaru prostych systemów astronomicznych prowadziła do większej dokładności opartych na nich przewidywań. Ale układy składające się z trzech i więcej ciał krążących po orbitach zachowywały się całkiem inaczej, zmniejszona niepewność pomiarów początkowych prowadziła do istotnie różnych rezultatów. Poincare doszedł do wniosku, że trafne przewidywanie złożonych układów można otrzymać tylko wtedy, jeśli posiadamy dokładne pomiary warunków początkowych, a jest to teoretycznie niemożliwe. Takie układy cechują się wrażliwością na warunki początkowe i nazywamy je dziś układami chaotycznymi, długoterminowe przewidywania matematyczne są tak samo trafne, jak przewidywania losowe.
Bardzo drobna, umykająca naszej uwadze przyczyna powoduje znaczny efekt, którego nie możemy nie zauważyć; mówimy wtedy, że efekt ten spowodowany jest przez przypadek. Gdybyśmy znali dokładnie prawa natury oraz sytuację wszechświata w chwili początkowej, bylibyśmy w stanie dokładnie przewidywać stan tego wszechświata w następnych chwilach. Jednak nawet wtedy, gdy prawa natury przestaną być dla nas sekretem, stan początkowy będziemy mogli poznać jedynie w przybliżeniu. — Henri Poincare

Dynamiczna niestabilność, czyli chaos
Pół wieku później, amerykański meteorolog, Edward Lorenz postanowił, że uda mu się przewidzieć długoterminową pogodę. Skoro przy pomocy komputera można było obliczyć dokładne trasy lotów pocisków i statków kosmicznych, to dlaczego nie zastosować tego do pogody?
W 1961 bawił się swoim symulatorem pogody, ale tego dnia razem zrobił coś nowego. Jego program komputerowy działał z dokładnością sześciu miejsc po przecinku, więc wynik wyglądał przykładowo tak: 0,123456. Zamiast wystartować program symulujący pogodę, zaokrąglił ostatnio otrzymaną zmienną 0,506127 do trzech miejsc po przecinku. Według niego, wynik miał wyglądać i tak identycznie jak poprzedni, przecież zaokrąglona wartość 0,506 nie zrobi różnicy. Pogoda powinna ewoluować w taki sam sposób za każdym razem. Poszedł po kawę i kiedy wrócił odkrył, że wykres w pewnym momencie zaczyna się różnić od pierwszego. Nałożył więc na siebie obydwa. Początkowo dwa szczyty na obu wykresach dokładnie pasowały do siebie. Potem jeden zaczął pozostawać w tyle, aż przy trzecim szczycie całe podobieństwo zniknęło:
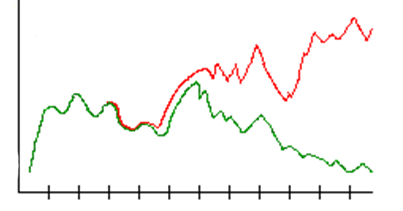
Lorenz zaobserwował empirycznie, że istnieją systemy, które wykazują nieprzewidywalne zachowanie (i wcale nie znaczy to, że nie podlegają żadnym prawom fizyki).
Efekt motyla
Lorenz zrozumiał, że pogody nie da się przewidywać. Mały błąd numeryczny w układzie równań zmieniał całkowicie wynik. Lorenz nazwał takie działanie Efektem Motyla (trzepot skrzydeł motyla w Brazylii powoduje tornado w Teksasie — najmniejsza zmiana w punkcie wejścia może doprowadzić do znacząco różnych wyników). Ciekawostka, efekt motyla najpierw nazywał się efektem mewy.

Układ deterministyczny może zachowywać się chaotycznie, jeśli jest wrażliwy na warunki początkowe. W takim wypadku, jeśli początkowe błędy wzrastają, układ jest chaotyczny i przewidzenie jego ewolucji jest niemożliwe. Niemal każdy rzeczywisty układ dynamiczny, odpowiednio napędzany, okazuje się chaotyczny.
Czym jest chaos? Jedna z teorii mówi, że chaos to stochastyczne zachowanie występujące w układzie deterministycznym. Systemy chaotyczne są wrażliwe na warunki początkowe, ale przy tym wciąż są kierowane przez równania, nie są przypadkowe. Chaos jest samowolnym zachowaniem całkowicie rządzonym przez prawa fizyki. Czasem zachowanie chaotyczne może być ukryte przez bardzo długi czas, system wydaje się stabilny i przewidywalny, aż tu nagle bęc! Nagle wszystko się zmienia np. odwrócenie biegunów magnetycznych Ziemi (ostatni raz stało się to około 780 tysięcy lat temu). W naturze zjawiska chaotyczne są na porządku dziennym. Widzimy je nie tylko w pogodzie, ale i w ekonomii, aerodynamice, biologii populacji, termodynamice, chemii.
Atraktory
Wiemy już czym jest, chaos, ale pewnie zastanawiacie się, czym jest ten obrazek przypominający motyla, pojawiający się często przy okazji teorii chaosu. Jest to atraktor. Atraktory istnieją dwa, zwykły oraz dziwny.

Żeby łatwiej było zrozumieć koncept dziwnego atraktora, przedstawię go na podstawie naszej uroczej Chloe Price. Załóżmy, że Chloe ma mniej więcej tyle samo durnych pomysłów, które kończą się jej śmiercią (i Max musi cofać czas, aby ją ocalić), co pomysłów, które nie kończą się tragedią. Jest zachowana równowaga — atraktor. Wyobraźmy sobie, że Chloe postanawia iść postrzelać do butelek. Super pomysł! Ale Chloe strzela sobie w brzuch i Max musi cofać czas. Potem Chloe postanawia się zakraść na basen, na szczęście tym razem żyje. Chloe postanawia położyć się na torach. Genialne! Tylko, że znów kończy się tragicznie i Max znów ją ratuje. I tak w kółko Macieju.
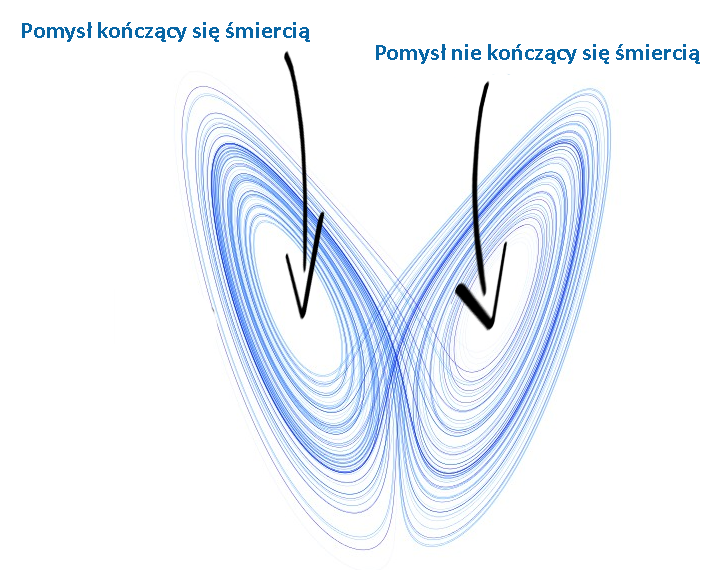
Różnica pomiędzy Atraktorem a Dziwnym Atraktorem jest prosta: atraktor reprezentuje stan, który ostatecznie osiada, dziwny atraktor opisuje tor, na którym system działa od sytuacji (super pomysł i śmierć!) do sytuacji (mądrzejszy super pomysł), ale bez osiadania.
Dlaczego efekt motyla w kulturze masowej jest zawsze źle interpretowany?
Efekt motyla przedstawiany w mediach, nie jest do końca tym, co miał na myśli Lorenz. W filmach, grach itp. efekt motyla to metafora istnienia zdarzeń pozornie nieistotnych, które zmieniają historie i przeznaczenie. Pisałam w poprzednim odcinku, że nie ma takiego czegoś jak przeznaczenie, a demon Lapleace’a nie istnieje. Jaki jest zatem problem z efektem motyla? Chodzi o to, że zgodnie z teorią Lorenza nie jesteśmy w stanie wyśledzić przyczyny zmiany. Nie możemy z całą pewnością powiedzieć, co spowodowało burzę. Jest przyczyna i skutek, ale nigdy nie będziemy w stanie odkryć, co dokładnie spowodowało ten skutek. Max, tornado nie zrobiło się przez ciebie! Mogło na nie wpłynąć milion przyczyn!
W kolejnym odcinku powrócimy do świata kwantów. Będzie o wszechświatach równoległych. I kocie. Zawsze musi być o kocie.



